Nombor Bahagi x
Persamaan seperti 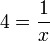 sebenarnya bukan linear tetapi boleh ditukarkan kepada bentuk linear dengan langkah yang sama yang telah dipelajari
sebenarnya bukan linear tetapi boleh ditukarkan kepada bentuk linear dengan langkah yang sama yang telah dipelajari
Latihan 12
Selesaikan
- a)
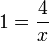
- Jwp :
- Peny :
- b)
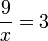
- Jwp :
- Peny :
- c)
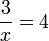
- Jwp :
- Peny :
- d)
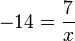
- Jwp :
- Peny :
- e)
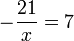
- Jwp :
- Peny :
- f)

- Jwp :
- Peny :
- g)
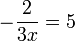
- Jwp :
- Peny :
- h)
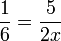
- Jwp :
- Peny :
Bandingkan
Bandingkan
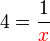 di bawah. Pada jawapan akhir, ianya tidak boleh di bawah. Jadi langkah pertama ialah
di bawah. Pada jawapan akhir, ianya tidak boleh di bawah. Jadi langkah pertama ialah  untuk didarab
untuk didarab(ovalbox(x))).png)
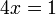
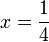
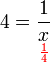
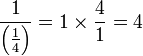
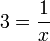
(ovalbox(x))).png)
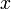 ke atas, nombor yang ada pada kedudukan itu (
ke atas, nombor yang ada pada kedudukan itu (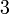 ) akhirnya perlu dipindahkan ke bawah pula. Jadi, kita juga boleh buat kedua-dua langkah ini sama-sama
) akhirnya perlu dipindahkan ke bawah pula. Jadi, kita juga boleh buat kedua-dua langkah ini sama-sama%3dfrac(1)(ovalbox(x))).png)
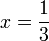
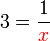 dipindah ke atas
dipindah ke atas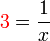 dipindah ke bawah
dipindah ke bawah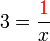 disalin
disalin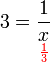
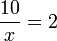
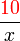 ?
?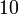 ,
, 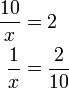
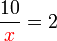 di bawah, jadi langkah pertama ialah
di bawah, jadi langkah pertama ialah (ovalbox(x))%3d2).png)
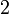 pula akan mengacau
pula akan mengacau (ovalbox(x))%3dovalbox(2)).png)
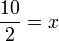
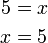
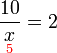
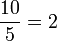 Betul
Betul
(ovalbox(x))%3dovalbox(3)).png)
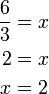

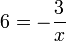
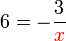 perlu dipindahkan
perlu dipindahkan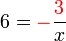 ditinggalkan
ditinggalkan(ovalbox(x))).png)
%3d-frac(3)(ovalbox(x))).png)
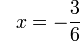
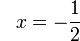
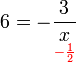

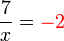
(ovalbox(x))%3dovalbox(-2)).png)
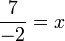
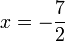
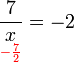
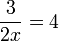
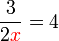 yang perlu dipindahkan
yang perlu dipindahkan(2ovalbox(x))%3d4).png)
(2ovalbox(x))%3dovalbox(4)).png)
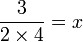
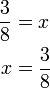
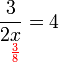

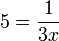
%3dfrac(1)(3ovalbox(x))).png)
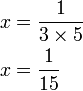
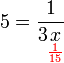


%3dfrac(4)(ovalbox(x))).png)

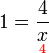
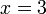
(ovalbox(x))%3dovalbox(3)).png)
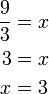
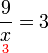
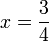
(ovalbox(x))%3dovalbox(4)).png)
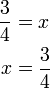
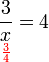
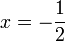
%3dfrac(7)(ovalbox(x))).png)
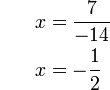
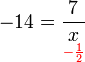
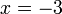
(ovalbox(x))%3dovalbox(7)).png)
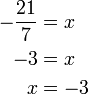
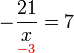

%3d-frac(10)(ovalbox(x))).png)
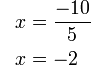
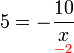
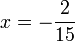
(3ovalbox(x))%3dovalbox(5)).png)
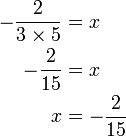
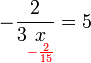
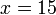
(6)%3d-frac(5)(2ovalbox(x))).png)
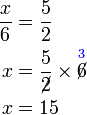
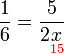
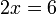
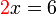
x%3d6x%3dfrac(6)(2)).png)
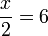
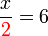
(ovalbox(2))%3d6x%3d6times2).png)
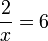
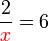 di bawah
di bawah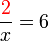 BUKAN masalah utama dan tiada gunanya kita pindahkan
BUKAN masalah utama dan tiada gunanya kita pindahkan(ovalbox(x))%3dovalbox(6)frac(2)(6)%3dx).png)
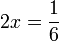
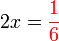 perlu
perlu 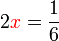
x%3dfrac(1)(6)x%3dfrac(1)(6times2)).png)
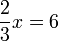
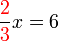
)(ovalbox(3))x%3d6)x%3dfrac(6times3)(2).png)
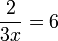
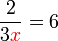
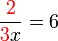
(3ovalbox(x))%3dovalbox(6)frac(2)(3times6)%3dx).png)
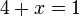
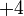 dipindah
dipindah%2bx%3d1x%3d1-4).png)
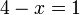
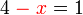 , dipindah untuk hapuskan negatif dulu
, dipindah untuk hapuskan negatif dulu%3dovalbox(%2b1)4-1%3dx).png)
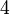 dipindah
dipindahx%3d1x%3dfrac(1)(4)).png)
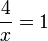
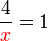 di bawah, dipindah ke atas ke sebelah
di bawah, dipindah ke atas ke sebelah(ovalbox(x))%3dovalbox(1))frac(4)(1)%3dx).png)